Écart type géométrique

Dans les domaines des statistiques et des probabilités, l'écart type géométrique décrit la dispersion d'un ensemble de nombres autour de la moyenne géométrique.

Définition

Si la moyenne géométrique d'un ensemble de nombres {A₁, A₂, ..., A_n} est notée μ_g, alors l'écart type géométrique est défini par :

\sigma _{g}=\exp \left({\sqrt {\sum _{i=1}^{n}(\ln {A_{i} \over \mu _{g}})^{2} \over n}}\right).\qquad \qquad (1)

où

\mu _{g}={\sqrt[{n}]{A_{1}A_{2}\cdots A_{n}}}.\,

Preuve

on a

\ln \mu _{g}={1 \over n}\ln(A_{1}A_{2}\cdots A_{n}).

\ln \mu _{g}={1 \over n}[\ln A_{1} \ln A_{2} \cdots  \ln A_{n}].\,

$\ln \,\mu _{g}$ est donc la moyenne arithmétique de $\{\ln A_{1},\ln A_{2},\dots ,\ln A_{n}\}$ , par conséquent l'écart type de cet ensemble de nombres est :

\ln \sigma _{g}={\sqrt {\sum _{i=1}^{n}(\ln A_{i}-\ln \mu _{g})^{2} \over n}}

d'où

\sigma _{g}=\exp {\sqrt {\sum _{i=1}^{n}(\ln {A_{i} \over \mu _{g}})^{2} \over n}}

Lien avec la loi log-normale

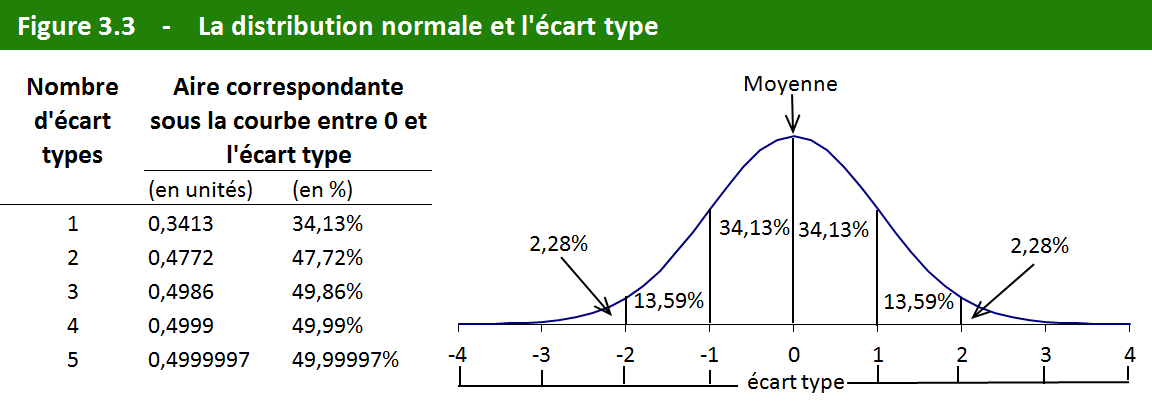
L'écart type géométrique est relié à la loi log-normale. Celle-ci est une distribution de Laplace-Gauss pour les variables $Y=lnA$ ; A suit alors une loi log-normale. L'écart type géométrique est donc l'exponentielle de l'écart type de Y, puisque $\ln \mu _{g}$ est la moyenne de Y.

Ainsi, la moyenne géométrique et l'écart type géométrique sont deux grandeurs pouvant être utilisées pour trouver les bornes d'un intervalle de confiance pour la distribution log-normale, d'une manière identique à ce qui est fait pour la loi normale.